Oscillateur de Van der Pol

En physique, lorsque l'on étudie un phénomène, on s'intéresse généralement d'abord aux effets prépondérants de celui-ci. Ceci revient souvent à linéariser les phénomènes caractéristiques du système étudié (on dit qu'il y a proportionnalité entre la cause et l'effet). Les effets non linéaires sont souvent considérés comme perturbatifs et de ce fait négligés, ils conduisent cependant quelquefois à des effets spectaculaires. On se propose d'étudier quelques-uns uns de ces effets et leurs représentations dans différents systèmes de coordonnées, à travers l’équation de l’oscillateur de Van der Pol.

I.Introduction

Le pendule simple :


L’application des théorèmes fondamentaux de la mécanique conduit à la mise en équation suivante : en admettant bien sûr que la liaison est parfaite et qu'il n'y a aucun frottement. Si on veut rendre compte de la puissance dissipée par frottements on peut ajouter un terme dépendant de . Il faut noter que cet oscillateur n'est pas linéaire sauf pour les petits angles où l'on peut faire l'approximation suivante : approximation valable au deuxième ordre en q .
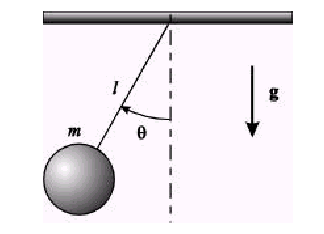
L'équation différentielle s'écrit alors :


avec
L’oscillateur de Van der Pol
Nous savons que, pour que les oscillations puissent prendre naissance au niveau du système, il était nécessaire que dans l'équation différentielle le coefficient devant le terme du premier ordre soit négatif. Ensuite pour que ces mêmes oscillations soient limitées en amplitudes il faut que ce coefficient change de signe, le système évolue alors sur un cercle limite. C'est l’idée qui est à la base de l'oscillateur de Van der Pol que nous allons étudier.
M. Van der Pol propose l'équation différentielle suivante :


où sont des constantes caractéristiques du système.
Si on analyse cette équation on constate que pour des amplitudes faibles la fraction est négligeable devant l’unité et l'équation différentielle se ramène à une équation différentielle correspondant à la naissance d'oscillations dont l'amplitude croît exponentiellement puisque le coefficient du terme du premier ordre est .
Lorsque l'amplitude de ces oscillations est importante la fraction devient supérieure à l’unité et le terme change de signe, l'amplitude des oscillations décroît exponentiellement, le système évolue alors entre deux états limites infiniment proches qui définissent l'amplitude et la forme des oscillations.
On comprend déjà intuitivement que le terme en sera responsable de la valeur de l'amplitude des oscillations alors que va influer sur le caractère plus ou moins sinusoïdal de celles-ci.
De plus, si l’on veut tenir compte d’un forçage extérieur sur l’oscillateur, nous devons introduire dans le membre de droite de l’équation précédente la quantité et il vient :


avec .
Cette équation peut être réécrite sous forme d’un système différentiel autonome :


avec .

II.Analyse numérique de l’oscillateur de Van der Pol non forcé

1. Etudes préliminaires
L’oscillateur non forcé revient à étudier l’équation :


Soit sous la forme du système autonome, on peut écrire :


On peut donc calculer les éventuels points fixes :


Nous avons donc un point fixe unique : (x,y)=(0,0). Pour étudier la stabilité de ce point fixe, nous introduisons la matrice Jacobienne du système autonome :


Pour le point (x,y)=(0,0) on a donc :


La nature du système dépend de la trace de la matrice Jacobienne. Ici, nous avons clairement 3 cas selon le signe de e . Pour un e positif ou négatif le système est dissipatif ((0,0) est un point répulsif ou attractif), pour e =0 le système est conservatif ((0,0) est un centre). Qualitativement, comme e représente le frottement, si celui ci est faible, nous aurons un caractère oscillatoire, donc des valeurs propres complexes de la Jacobienne et le point stable sera un foyer. Vérification quantitative, équation aux valeurs propres :


En résumé :

• ï e ï <2
e <0 Þ (0,0) foyer attractif
e =0 Þ (0,0) centre
e >0 Þ (0,0) foyer répulsif

• ï e ï >2
e <0 Þ (0,0) nœud stable
e >0 Þ (0,0) nœud instableQualitativement, e =0, nous avons une bifurcation de Hopf supercritique puisque , en zéro on passe d’un foyer stable à un foyer instable.
2.Simulation numérique

fig.1                                                                fig.2

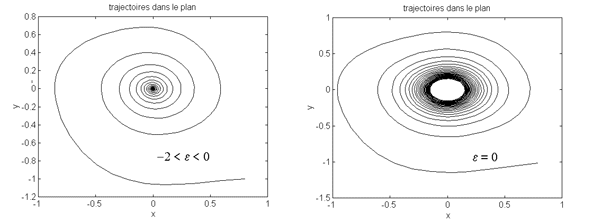
fig.3                                                                fig.4

fig.5                                                                fig.6

Les simulations numériques rendent bien comptes des prédictions analytiques. Il est à noter cependant l’apparition d’un cercle limite stable pour le cas 0<e <2 due à la limitation d’amplitude introduite par le terme de frottement quadratique (donc non linéaire). On a donc bien une bifurcation de Hopf supercritique pour e =0.

III.Analyse numérique de l’oscillateur de Van der Pol forcé

1. Etudes préliminaires
Il nous faut donc ici étudier l’équation :


Equation que l’on peut réécrire sous la forme d’un système différentiel autonome comme :


Il apparaît de manière évidente que le point (a,0,0) est point fixe de ce système.

2. Simulation numérique
Etant donné que e est légèrement positif, les trajectoires divergent en spirale au voisinage de l’origine. Dans cette région, q est toujours très petit et le terme en q ² reste donc négligeable. A grande distance de l’origine, par contre, les trajectoires ont tendance à se rapprocher du point fixe puisque le terme (e -x²) est alors négatif. On conçoit intuitivement qu’il existe entre ces deux extrêmes un cycle limite. D’où la forme des trajectoires dans l’espace des phases (fig. 5 à 8).

fig.7                                                                fig.8

Le paramètre e influence la forme de l’orbite périodique. Pour e =0 on retombe sur l’oscillateur harmonique et on a donc une trajectoire circulaire (trivial). Lorsque e est plus grand, le cycle limite est presque rectangulaire (fig.7). Son parcours fait donc intervenir deux échelles de temps distinctes.
Le coefficient " a " (s’il est assez grand pour être perceptible) de forçage impose une régularité sur ces échelles par rapport à sa fréquence (fig.8).
Nous avons vu précédemment qu’il existait une bifurcation de Hopf quand e change de signe. On a donc un tore T² comme attracteur, au moins au voisinage de la bifurcation.


fig.9
Dans une analyse de Fourier du signal temporel continu, on s’attend donc à trouver deux pulsations distinctes, correspondant aux périodes des mouvements le long du grand cercle et du cercle de gorge. Si ces deux fréquences sont dans un rapport rationnel, on s’attend à observer le phénomène d’accrochage de fréquences et trouver un nombre d’ " harmoniques " égal à ce rapport, comme l’illustre les résultats si dessous.

fig.10                                                                fig.11

fig.12                                                                fig.13

Il est assez aisé de compter " à l’œil " ce nombre de fréquences différentes dans le cas où il ne serait pas trop grand (fig.10 à 12). Pour un rapport plus grand, cela devient moins évident (fig.13). Mais si l’on procède à une transformation intégrale type transformée de Fourier, il apparaît un pic pour chaque fréquence présente dans le spectre, comme le montre le résultat suivant :


fig.14
Si maintenant, on considère une rapport de la fréquence propre de l’oscillateur et du forçage irrationnel, le spectre de Fourier du signal quasi périodique correspondant présente a priori une infinité dense de raies à toutes les pulsations , où n₁ et n₂ sont des entiers.
Cependant, la simulation numérique n’est qu’un échantillonnage de valeurs discrètes et qui plus est arrondies. Ce qui entraîne irrémédiablement que le spectre de Fourier ne présente pas l’infinité denses de raies. Il faudrait pour cela faire une simulation sur un nombre de rotations infini et une meilleure approximation des nombres irrationnels.

fig.15                                                                fig.16

Visuellement (fig.15), on s’aperçoit que pour une durée relativement courte de la simulation numérique, il apparaît un mouvement périodique, avec toujours les deux fréquences de parcours du tore. Ceci se répercute bien sûr au niveau du spectre de Fourier, où l’on peut distinguer plusieurs pics. Celui ci est tout de même plus erratique et dense que pour un rapport rationnel (fig.14), ce qui tend à confirmer les propriétés énoncées plus haut.

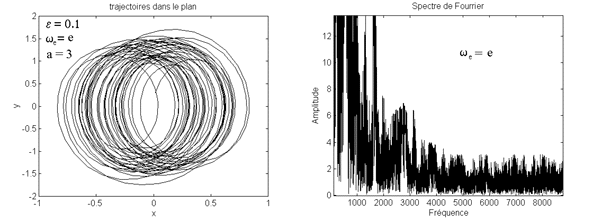
fig.17                                                                fig.18

Les résultats sont bien plus probants avec le nombre e. En effet, le spectre de Fourier présente bien une infinité de raies denses (fig.18).

III.Concusion
Le pendule forcé et gêné est la schématisation quasi générale de l’oscillateur. Ces systèmes périodiques sont extrêmement répandus, que ce soit un électron gravitant autour de l’atome d’un cristal plongé dans un champ magnétique ou un rythme biologique (respiration, contraction du muscle cardiaque, alternance de veille et de sommeil, cycle de reproduction des plantes, etc.). La clef de l’analyse de tous ces phénomènes est l’oscillateur.
L’équation de Van der Pol est une modélisation du mouvement de bon nombre de ces systèmes oscillatoires. Nous avons vu dans ce travail, que selon la valeur des paramètres de cette équation, les trajectoires avaient des caractéristiques bien précises.
Ainsi, le paramètre e de frottement joue un rôle essentiel. L’oscillateur présente une bifurcation de Hopf normale (ou supercritique), lors du passage d’une situation où le système passe d’un état attractif à un état répulsif (e change de signe). Il se passe ensuite le phénomène d’accrochage de fréquence selon la valeur de la fréquence du forçage par rapport à la pulsation propre de l’oscillateur harmonique.
BIBLIOGRAPHIE :
-P. BERGE, Y. POMEAU, Ch. VIDAL ‘L’ordre dans le chaos’ Hermann (1984)
-James GLEICK ‘La théorie du chaos’ Albin Michel (1989)
-‘La science du désordre’ La Recherche (mai 1991) p539 à 552
-‘Le chaos, monstre sensible et docile’ Science&Vie (nov 1993) p38 à 45
-‘Turbulence dans une boîte’ La Recherche (mai 1991) p628 à 638
-‘La diffusion chaotique’ La Recherche (avr 1989) p490 à 498
-‘Le ciel est imprévisible’ Science&Vie (nov 1993) p46 à 55
-‘La revanche du dieu chaos’ La Recherche (mai 1991) p542 à 549
-‘La maîtrise du chaos’ Pour la Science (oct 1993) p64 à 70
-‘La physique du désordre’ La Recherche (mai 1991) p554 à 570
-‘Le chaos en biologie’ La Recherche (mai 1991) p588 à 598
-‘Des billards au chaos des atomes’ La Recherche (mai 1991) p600 à 608
-‘Le chaos dans le système solaire’ La Recherche (mai 1991) p572 à 582
-‘Les désordres boursiers’ La Recherche (mai 1991) p668 à 672
-‘Henri Poincaré, le précurseur’ La Recherche (mai 1991) p566 à 570