Le filtre RC comme son nom l'indique est composé d'une résistance et d'un condensateur.
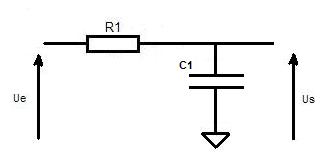
Le produit de R par C est appelé constante de temps du circuit.
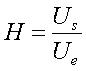
Pour calculer la fonction de transfert du filtre passe bas, nous calculons la tension de sortie à l’aide des formules du pont diviseur :
Zc est l’impédance du condensateur. w est la pulsation = 2 x pi x f
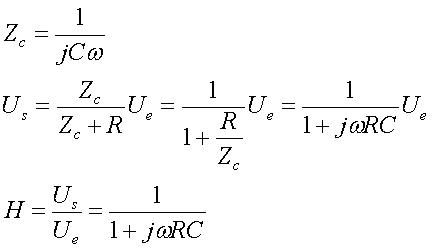
H est complexe : (présence de j)
- le module de H est le gain = sqrt(a²+b²) (H= a+jb)
- la phase est tan(phi)=a/b (H=a+jb)
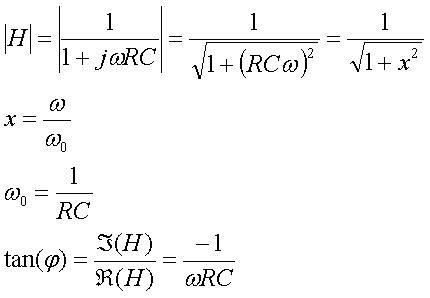
Attention : tous ces calculs ne sont valables que si l’impédance de sortie (en parallèle de Us) est infinie. Si on place un composant en sortie, ce dernier aura une impédance qui devra être prise en compte dans les calculs. Les formules deviennent alors bien plus complexes.
Si on trace le diagramme de Bode de la formule du gain, nous obtenons la courbe suivante :
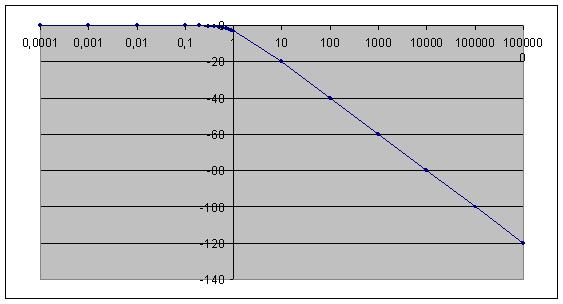
Si w = w0 dans ce cas le gain est de –3dB (en tension, la formule est 20log(G)).
Cette courbe représente le cas idéal, avec des composants parfaits. Dans la réalité, il faudra tenir compte des éléments parasites des composants : (donnés à titre indicatif, voir les spécification des fabricants).
- pour une résistance CMS classique : 300fF de capacité parasite parallèle, 2nH d’inductance série
- pour le condensateur CMS céramique : 10mOhm d’ESR, 2 nH d’inductance parasite série, 50Mega Ohm de résistance parallèle.
Ainsi la courbe obtenue n’est plus exactement celle que nous venons de voir :
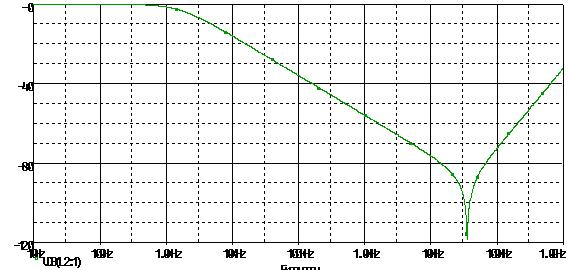
Nous observons qu’au delà d’une certaine fréquence (ici environ 30 mégahertz), le circuit RC devient un passe haut.
Une fréquence parasite de 1GHz ne verra donc que 30 à 40 dB d’atténuation, alors que la fréquence de coupure de ce filtre est de 1.5kHz ! (10kOhm, 10nF)
Pour des montages pointus, il faudra veiller à bien soigner le routage ainsi que le choix des composants. Ceci afin de minimiser les composants parasites.
Note concernant l’impédance de charge : que se passe t-il si nous chargeons ce filtre par une résistance idéale de 100kOhm par exemple (courbe rouge).
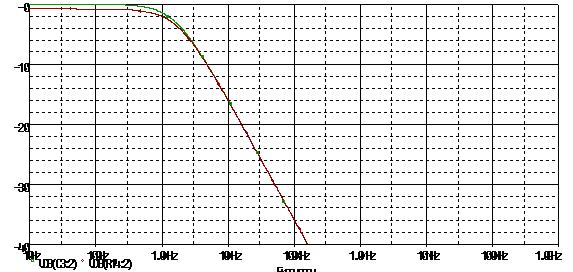
Dans ce cas nous remarquons une atténuation non négligeable dans la bande passante du filtre (environ 1dB).
Ensuite la pente est respectée.
Filtre RC passe bas:

Le produit de R par C est appelé constante de temps du circuit.
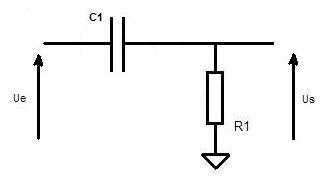
Filtre RC passe haut:

Fonction de transfert du filtre RC passe bas :
La fonction de transfert H est le rapport entre la tension de sortie Us et la tension d’entrée Ue :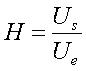
Pour calculer la fonction de transfert du filtre passe bas, nous calculons la tension de sortie à l’aide des formules du pont diviseur :
Zc est l’impédance du condensateur. w est la pulsation = 2 x pi x f
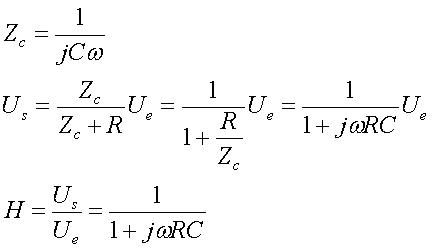
H est complexe : (présence de j)
- le module de H est le gain = sqrt(a²+b²) (H= a+jb)
- la phase est tan(phi)=a/b (H=a+jb)
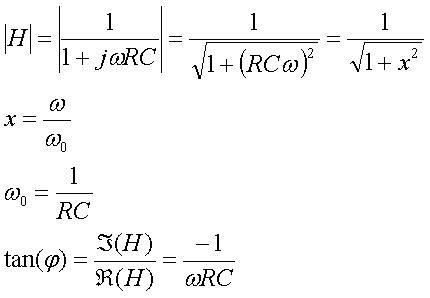
Attention : tous ces calculs ne sont valables que si l’impédance de sortie (en parallèle de Us) est infinie. Si on place un composant en sortie, ce dernier aura une impédance qui devra être prise en compte dans les calculs. Les formules deviennent alors bien plus complexes.
Si on trace le diagramme de Bode de la formule du gain, nous obtenons la courbe suivante :

Si w = w0 dans ce cas le gain est de –3dB (en tension, la formule est 20log(G)).
Cette courbe représente le cas idéal, avec des composants parfaits. Dans la réalité, il faudra tenir compte des éléments parasites des composants : (donnés à titre indicatif, voir les spécification des fabricants).
- pour une résistance CMS classique : 300fF de capacité parasite parallèle, 2nH d’inductance série
- pour le condensateur CMS céramique : 10mOhm d’ESR, 2 nH d’inductance parasite série, 50Mega Ohm de résistance parallèle.
Ainsi la courbe obtenue n’est plus exactement celle que nous venons de voir :

Nous observons qu’au delà d’une certaine fréquence (ici environ 30 mégahertz), le circuit RC devient un passe haut.
Une fréquence parasite de 1GHz ne verra donc que 30 à 40 dB d’atténuation, alors que la fréquence de coupure de ce filtre est de 1.5kHz ! (10kOhm, 10nF)
Pour des montages pointus, il faudra veiller à bien soigner le routage ainsi que le choix des composants. Ceci afin de minimiser les composants parasites.
Note concernant l’impédance de charge : que se passe t-il si nous chargeons ce filtre par une résistance idéale de 100kOhm par exemple (courbe rouge).

Dans ce cas nous remarquons une atténuation non négligeable dans la bande passante du filtre (environ 1dB).
Ensuite la pente est respectée.
Aucun commentaire:
Enregistrer un commentaire